
As requested by someone, I want to talk about Stephen Hawking's work! It's a challenge, because I am not a physicist. But, I am closer to the subject than the average person, so let's see if my understanding of mathematics (especially differential equations) can help translate whatever Stephen Hawking talked about.
Unless it is cited, I am relying mostly on random facts I’ve learned. I apologize if real physicists ever come across this amateur article. But, let’s get started!

From what I understand, Stephen Hawking’s defining topic is Black Holes. While scientists have confirmed the existence of black holes in 1971 with Cygnus X-1 (NASA article), there is still so much to learn and confirm about them.
In my time in Mathematics (and some random YouTube videos), I have heard that black holes are objects with immense gravitational force, where space collapses down to a point in its center and that once you’re past the ``event horizon’’, you’re done. So, let’s talk about this one by one.
Force is anything that can accelerate an object. Accelerate means to change its velocity. For example, something can be standing still and a wind blows it away. Its velocity went from 0 to maybe 1 mile per hour, it has accelerated. Another example is driving on the street at 25mph and going on the highway going 45mph. You change your speed and so you have accelerated. In both of these situations, force has acted (wind or engine in your car).
Then, from our point of view, gravitational force is the force that pushes things down to the ground. It accelerates everything to the surface of the planet. Why or how it happens? I don’t know. But, in space or outside of our point of view as humans, gravitational force is all about accelerating objects towards one another. It’s different from a magnet, but you can certainly imagine that if you’d like.
So, black holes have immense gravitational force, which means if anything gets close to it, it will force it towards itself. What’s cool or maybe grim about this is that it is one of the strongest forces in the universe, so not even all of Earth’s population playing tug-of-war could save whatever falls into the influence of black holes. This is what I believe is the event horizon, it’s the rim around the blackhole where your escape is futile.
``Collapse down to a point’’ is actually still debated! This is one of those things that we (Physicists and Mathematicians) believe to be true. Essentially speaking, with the immense gravitational force that black holes have and its insisting that you get closer and closer and closer, you’ll just keep falling and falling and falling. But, the geometry of space is so weird (and unconfirmed) inside of a black hole that many fictional depictions of black holes have it as a funnel. At the center of that funnel is believed to be a single point. Have fun being crushed into something smaller than a piece of sand!

So, what does Stephen Hawking talk about with this crazy object in the universe? One of the first things I came across was his Area Theorem (Wikipedia Article) which actually fights the Second Law of Black Hole Thermodynamics! If you looked at the link, the Second Law states:
The derivative is a way to talk about “instant change”. To wrap our minds around this, the example Calculus students usually work with is the difference between average speed versus instant speed. If we were to drive five miles in 10 minutes, you could say that your average speed is half a mile every minute. This is your average change (in distance)! But, what if we actually sped up through those 10 minutes, maybe we spent the first five minutes driving slowly but we sped for the second half to still make 5 miles in 10 minutes! (See the picture below.) Even though we still have the same average speed, we have a different instant speed depending on where we were. So, you can roughly think of the derivative as being a more accurate statement of information at any given time in your journey.
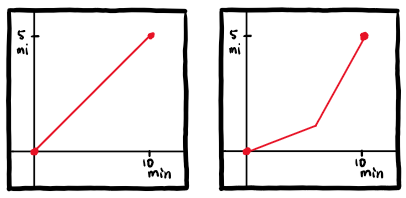
So, $\frac{dA}{dt}$ is saying “the instant change of A(rea) in time” and by making it greater than or equal to 0, the Second Law is saying that the instant change of Area at any given time is always going to be positive or zero. If you want to use the speed analogy again, we never allow ourselves to drive backwards! You can stop driving, but never drive in reverse.
For the black hole, its “horizon area” is never going to go backward (a.k.a. lose area)! Horizon area, I’m assuming, refers to how big and wide the event horizon is (the point of no return).
Hopefully the statement makes sense now! (We’re ignoring what the weak energy condition is.) But, what Stephen Hawking found is that this is NOT true!!! Woah!
From what I’ve read and watched, Stephen Hawking found that the instant change of the horizon area of a black hole is in fact able to go negative! It’s able to lose area, it’s able to shrink… meaning black holes are able to die… at some point. They will still outlive everything else in this universe, so they will still live a long life. Stephen Hawking found that black holes radiate their mass out and that’s cool. The analogy here is like water evaporation. A more gross example is when your body sweats, it is losing water mass.
That’s pretty much the extent of what I learned about all these things in the day I spent writing this. Hopefully this made some sense and maybe you’ll go on to be able to watch black hole videos with more understanding. Thank you for reading this!
Uploaded 2023 July 28. This is a part of a monthly project which you can read about here.