One of my friends asked me with the urgency of life and death, “HOW DO YOU TEST FOR PRIME NUMBERS[?!]”, and I heard alarms ringing in my head. Did I forget this very important test? In a weird coincidence, I had already planned to cover “prime numbers” this month.
Let’s back up for a moment, what is a prime number? A number such that the only number that can divide it without leaving a remainder is itself. Note that we are not calling the number 1 a prime number, this is a more special number called a “unit”. Prime numbers are special, because if you multiply two prime numbers X and Y, you get a number that only has X and Y that can divide it.
The short answer to my friend is no, there’s not a widely accepted way to test for prime numbers. In the short trek into “primality” tests [1], I found that there are computer programs that when given a physical number, it will tell you if it is prime. But, these aren’t quick algorithms. Depending on the size of your number (tens of digits), it could take longer than a second for the program to answer you. And in programming, a second is too long (since it adds up).
But why is this an important question to answer quickly?
If we can create a machine that can answer the question “Is this prime?” in an instant, then passwords and security would be shattered. (Dramatization for effect.) If hackers had access to an almost-instantaneous machine that could answer “Is this prime?”, then they could test millions of prime numbers relatively quickly to break passwords.
Let’s back up again. How are prime numbers able to break passwords?
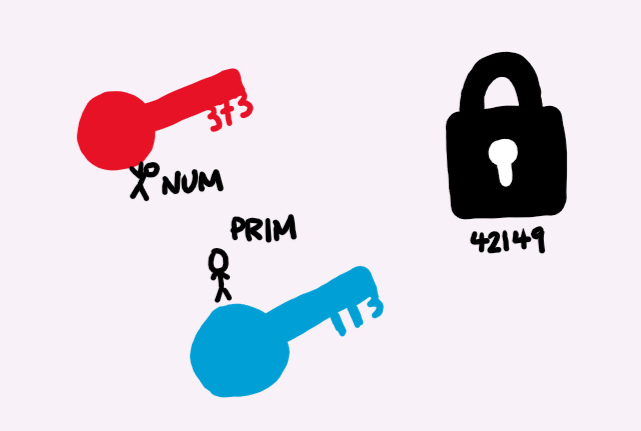
Imagine two people, call them Prim and Num, and they have a private chat. Now Prim and Num have a smart idea of choosing two prime numbers as the keys for accessing their private chat. Let’s say Prim chose the prime number 113 and Num chose 373, then they set the lock to be the product of 113 and 373 (42149). Their private chat will only open if you feed it a number (greater than 1 and less than the number itself) such that dividing the number in the lock with the number you gave will return no remainder. Test it out, divide 42149 by any number that isn’t 113 or 373, you’ll get an answer with decimals (meaning there’s a remainder!!).

This is sort of a very simple example, but you can already make this more complex. You can make your prime numbers be more than ten digits so the product becomes more than 100 digits. You can keep the number on the lock a secret. You can use other operations (exponents, logarithms, etc.) to relate Prim and Num’s numbers. You can add layers upon layers that spiral further. The idea here is to have an easy way from start to finish, but it is hard to go backwards from finish to start.
From what I gather, when you have a password, say “Pass123”. Security logins take that password and turn it into a mess of a mess of a number representation, maybe by the end of the process Pass123 becomes 67926357102836503826493. After that, the system checks if this messy number is a key to the lock that is on your account.
So, if we had this “Is this prime?” Prime machine that answered in an instant: this scenario can happen:
The Prime machine sped up the process, it didn’t completely break security, but this person now has saved a lot of time.
It’s all fascinating stuff, and my scenario is very simple in comparison to the complexity that goes into protecting and securing accounts and data. Studying prime numbers is one of the many intersections between Mathematics (number theory, graph theory, and coding theory) and Computer Science (cryptography, security, and coding theory).
The next part is anecdotal and it’s not really related to the discussion above. However, in this past month, my academic life has been a chaotic mess.
To add to that chaos, I have started reading for fun (very out of character for me). My professor, advisor, and forced-to-be-my-mentor mentor Rolando de Santiago gifted me Mathematics for Human Flourishing by Francis Su with reflections by Christopher Jackson [2]. Due to the chaos of this month and my conscious decision to savor this wonderful book, I have barely made it halfway through the book.
I bring this book to this discussion, because it made me think a lot about what I really want to accomplish with Monthly Math-y. Sure, at its heart, Monthly Math-y had two personal missions: 1) practice writing about math in an understandable way, and 2) get non-math-y people to understand that there’s depth and life in this field.
However, I think I haven’t been doing a great job at either, and I should focus on one goal as opposed to spreading myself thin. Francis Su sets out to convince the reader, using a dozen avenues, that “Mathematics” satisfies “Human Flourishing”. In a similar manner, I will set out to prove to you, my friends and peers, that the many subjects and subfields of math are interesting and have “real-life” consequences.
The ultimate mission is still personal and may be a little petty; to have this collection of writings to give to someone who asks “why do you study math, don’t we know everything about it already?”
[1] Wikipedia. Primarility Test. Accessed on March 2021: Asymmetric-key algorithms (link).
[2] Su, Francis. Mathematics for Human Flourishing with reflections by Christopher Jackson. Yale University Press, 2020. Francis Su's Website Link.
Uploaded 2021 March 31. This is a part of a monthly project which you can read about here
Diclaimer: With any type of work online, I do have to give a disclaimer: I am a math graduate student with a B.S. in Math, but I am not the end-all-be-all of this topic. I will most likely say something wrong, but the point of this project is to level math in a way that is understandable, perhaps at the cost of rigor and nuance.