Even I have to admit that jumping from “Induction” last month to “Topological Data Analysis” this month is a leap. However, two points: 1) this essay is to introduce you to the power that “Topology” has in real-life applications, and 2) I chose this topic to be a leap in order to challenge myself in reading and consuming math I am uncomfortable with. So, again, my hope for you is to finish reading this and get a “Oh okay, so that’s a thing” feeling, rather than a “I’m a master of topology now” feeling.
A textbook definition: a topology, denoted as T, on a set X is a set of subsets of X such that:
My translation of this: We have a box labeled X. A topology T on this box X are the different ways we can group just some of the things in the box and pull it out as if it was just one thing. Think of T as a set of rules of what you can grab out of the box X. The set of rules we have are
The third and fourth rules are probably the hardest to non-math-ify. So here’s an example to hopefully clarify it.
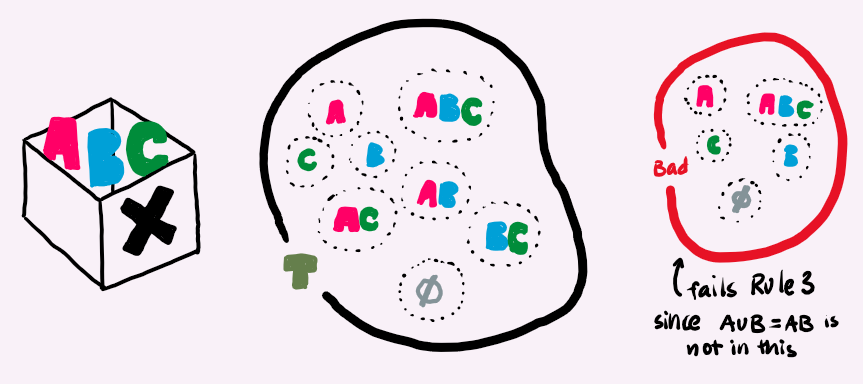
We have three things in X, maybe call them A, B, and C. A topology T for these three things would be another box that has objects: (empty), A, B, C, AB, AC, BC, and ABC. Then, we can see Rule 1 and 2 are fulfilled.
Let us demonstrate Rule 3: Take the objects AB and AC from T, then their union is ABAC, but we do not really care about the same object, so we just say it is ABC. In fact, ABC is in the list of things in T.
Now for Rule 4: We again take the objects AB and AC from T, then their intersection is A (since that is the only thing they have in common). Again, A is in the list of things in T.
So T is indeed a valid topology on X. Here is a cute drawing I did to represent this topology and also have another example that is not a real topology.

I cannot quite explain how these four rules evolved to be the useful and important field we have today. (It would be similar to explaining how the universe was formed from just protons, neutrons, and electrons.) But we should see topology as the study of “rubber sheet geometry”.
In this field, topologists study shapes and spaces that you stretch and shrink, but never cut or poke holes in. I mean, you can cut and poke holes, but you would be admitting that the shapes you had before and after are no longer the same “topologically”. So, topologists care a lot about the number of cuts or holes an object has, because this number should stay stable.
So, imagine a circle, topology knows that if we stretch the circle sideways that it is still relatively a circle. But, it also knows that if you cut and turn out the circle into a line that you lost the property that made it a circle.
Topology concerns itself with establishing and keeping the sanctity of shapes and spaces and the relations between them. With that concern for fragility, topology is one of the better tools for analyzing data.
Briefly speaking, data is what makes the (digital) world turn. It is how Netflix or Tiktok know which shows or videos to put on your front page. But, what is difficult about good data is that it is multidimensional. If you want to be a good data set, you have to be huge in detail.
Imagine a spreadsheet, like Excel, a good data set for something like TikTok or Netflix would have at least 10 columns (one for each characteristic) and millions of rows (one for each of the users). If you imagine each row as a dot in space, this is at least a 10-dimensional world you have to live in to capture the data’s true nature.
What makes things worse about data is that the people (or computers) analyzing it are “outsiders”, they did not make the data so they cannot influence what numbers they get. The task at hand is to analyze this 10-dimensional world when we only have a limited view of it.
Topology enters the picture, because data forms a shape in space and they have the tools to examine. There have been developments in reducing the complexity of dealing with multi-dimensions, as we’ll see later. Computers have gotten powerful that maybe 10-dimensions is not that hard to play with, but maybe there are thousands of columns. Topology plays a role in building a bridge between outsiders and that thousand-dimensional world.
Thus, Topological Data Analysis was born. In my attempt to learn more about this, I read two papers, listed below in the citations.
This section is less about going into the deep mathematics of these papers, but more about conveying the general information about them and why they matter in this discussion.
Robert Ghrist put the goals of topological data analysis (TDA) plainly as:
To go back to the thousand-dimensional discussion, TDA’s goal is to take perhaps 100 dimensions out of those thousand and use that to find more about the full world. After that inference, TDA builds a structure that is easier to work with (and keeps most of the sanctity of the thousand-dimensional world).
Ghrist supposes that data has a global shape that “often provide important information about the underlying phenomena that the data represent”. In this video of Professor Gunnar Carlsson at the Joint Mathematics Meetings (time stamp: 16:40), we can see an example of how shapes of data can provide insight on underlying phenomena.
Onto the next paper, Afra Zomorodian brings up another issue with data that I forgot to mention, and that data has noise. Noise for data are slight errors that damage the integrity of the original data. For the computer science students out there, Zomorodian name drops “IEEE floating-point arithmetic” having “discretization error” as one of the sources of data noise.
Zomorodian puts forth this idea that “in analysis, we try to recover intrinsic information, given only extrinsic information”, which goes back to the idea that we are outsiders of the data world and that we are doing our best to understand this higher dimension when we can only peak through the keyhole.
Before the sophistication and development of TDA, we had methods that made assumptions on the shape of the data clouds; assumptions that data have a straight-line relationship between each other. However, most real-world data are from spaces that do not obey the assumptions we made.
With TDA, we are given a “pipeline”, as Zomorodian puts it, in tackling data analysis. Given a finite set of points, (1) we first approximate the unknown space with a combinatorial structure. We have some points and know some things about them, so we make a graph to show the relationships.
Then, (2) we compute the topological invariants of the structure we made. We look for things we know that will not change about this graph if we were to broaden the view to a larger amount of data.
The idea in this TDA pipeline is we do not make a pre-assumption before seeing the data. We look at the data first, just a small part of it. We assume the structure of the smaller set, and with topology, we can build stable ways to learn what is happening in the larger world. This matters a lot because shape really does illuminate underlying behavior. Shape allows computers to make predictions, and predictions tie into marketing, social media, and other modern day society activities.
Oh okay, so that’s a thing.
In all seriousness, what I took away from this exploration is that topology (just like every other math field) has a spot beyond the academic sphere. Being aware of its power and place in modern day analysis and technological advancement adds to my appreciation of the field. Another thing to understand is that math likes to put itself second to what is given to it. It tries not to make an assumption on the object it is given, instead allows the object to guide its reasoning and next step. In a cheesy type of ending, I think that is just another reason why I really like math.
So, how exactly does the topology and math that Ghrist and Zomorodian wrote about work for data analysis? It hinges on this topology idea of “simplicial complexes”, which Zomorodian says is similar to a hypergraph. A graph is built out of nodes/vertices and edges/connections. On the other hand, a hypergraph is built out of notes/vertices, edges that connect two vertices, and what I’ll call super-edges, which can connect one vertex to a set of vertices.
In topology, we like to talk about open covers of a topological space. Let S be a finite set of data points, taken from our data cloud set X, embedded in some topological space Y. An open cover of S is a set U of open sets {U_i} with indexing set I such that each U_i is in Y and the union of these U_i is a superset of our set S.
Now, we have this added idea of a nerve. The nerve N of an open cover U = {U_i} must satisfy: (1) the empty (indexing) set is in N, and (2) if J is a subset of the indices I such that the intersection of {U_j} for j in J is non-empty, then J is in N. From what I understand, N is a set of sets of indices, and that N is a simplicial complex.
Zomorodian says that “the union of the sets in an open cover is our approximation of the unknown [data cloud set] X” and the nerve of U will be “the finite combinatorial representation”. Zomorodian also quotes Leray’s Nerve Lemma as something I can only understand as the reasoning why nerves are a good representation of data/point sets.
Ghrist and Zomorodian separately talk through different methods (complexes) on building these simplicial complexes, based on different structure qualities. For example, the Cech complex uses epsilon balls, while the Alpha complex uses the geometry of the embedding space Y alongside the epsilon balls.
Regretfully, the papers start to lose me at this point, if it has not already. The idea truly boils down to creating different nerves based on different open covers, motivated by the amount of leeway, power, and space we have. This accomplishes Zomorodian’s pipeline step (1).
If anything, this (non-topologist surface level) discussion should serve as a motivator for other (more appropriate) mathematicians to delve into this topic.
[1] Ghrist, Robert. Barcodes: The persistent topology of data. Published electronically in 2007 at the American Mathematical Society. Accessed on February 2021: AMS Journals 2008. Direct PDF link: here
[2] Zomorodian, Afra. Topological Data Analysis. Published in 2011. Accessed on February 2021: Proceedings of Symposia in Applied Mathematics, 2011 American Mathematical Society (link). Direct PDF link: here
Uploaded 2021 February 26. This is a part of a monthly project which you can read about here.
Diclaimer: With any type of work online, I do have to give a disclaimer: I am a math graduate student with a B.S. in Math, but I am not the end-all-be-all of this topic. I will most likely say something wrong, but the point of this project is to level math in a way that is understandable, perhaps at the cost of rigor and nuance.